Paraboloide de enfoque equilibrado para cocinas solares

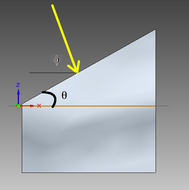
Recientemente, participé en una discusión sobre diseños de una cocina solar sencilla. El más obvio tiene un plato reflector paraboloide simétrico que enfoca la luz solar sobre la olla que se encuentra en el punto focal del paraboloide. El eje de simetría del paraboloide apunta al sol, por lo que el plato tiene que girar alrededor de un eje polar (paralelo al eje de rotación de la Tierra) a una velocidad de 15 grados por hora para seguir el movimiento diario del sol. el cielo. Este eje de rotación debe pasar a través de la olla, en el centro del plato, de modo que la olla permanezca estacionaria mientras el plato gira. El plato también debe poder inclinarse alrededor de un eje perpendicular, para seguir los movimientos estacionales del sol de norte a sur. Esta segunda rotación es muy lenta y se puede realizar reajustando manualmente el plato cada pocos días. La rotación más rápida debe ser impulsada por algún mecanismo, como un reloj. Si el plato debe tener una forma fija (a diferencia de un reflector Scheffler) y su foco debe permanecer en el eje polar mientras el plato se inclina alrededor del eje perpendicular, el eje perpendicular también debe pasar por el foco. Por tanto, los dos ejes de rotación deberían cruzarse en el foco.
Los mecanismos de reloj no producen mucho torque, por lo que preferiblemente el plato debe tener su centro de gravedad (o centro de masa) ubicado en el eje polar para que pueda girarse fácilmente. Para que el centro de gravedad permanezca en el eje polar cuando el plato se inclina respecto al perpendicular, el eje perpendicular también debe pasar por el centro de gravedad. Los dos ejes deben cruzarse en el centro de gravedad del plato.
Los dos párrafos anteriores implican que el centro de gravedad del plato y su foco deben ser el mismo punto. Las dimensiones del plato deben ser tales que su centro de gravedad coincida con su foco.
Suponiendo que el plato está hecho de un material de espesor uniforme, es decir, densidad de masa, calculé sus dimensiones requeridas. (Ver más abajo.) Usando F para denotar la distancia focal del paraboloide, resulta que la profundidad del plato, medida a lo largo del eje del paraboloide desde el vértice hasta el plano del borde, que es perpendicular al eje, es 1,8478 veces F. El radio del borde del plato es 2,7187 F. (La cercanía de este número al valor de "e", la base de los logaritmos naturales, es sólo una coincidencia accidental, pero constituye una herramienta mnemotécnica útil .) El radio angular del borde visto desde el punto focal es 72,68 grados.
Una simple cocina solar tendría un plato de este tipo, girado por un reloj alrededor de un eje polar. Se proporcionaría un segundo eje, perpendicular tanto al eje polar como al eje del paraboloide, para permitir girar el plato para seguir los movimientos estacionales del sol. Ambos ejes de rotación pasarían por el punto focal del plato.
Un brazo estacionario, unido a algún soporte externo al plato, alcanzaría el plato hasta su foco y sujetaría la olla por su extremo, en el punto focal. Idealmente, este brazo coincidiría con el eje de simetría del paraboloide cuando apunta al sol al mediodía en un equinoccio. El plato podría girar 72,68 grados antes de que el borde del plato choque con el brazo fijo. A 15 grados por hora, esto llevaría casi cinco horas. Por lo tanto, la cocina se podría utilizar aproximadamente desde las 7:15 hasta las 16:45 sin mover el brazo. En latitudes tropicales, esto corresponde más o menos a la parte completa del día en que el sol está lo suficientemente alto sobre el horizonte para que sea posible cocinar con energía solar. En épocas del año distintas de los equinoccios, habrá poca diferencia en el período en el que se puede utilizar la cocina.
Calcular las dimensiones del paraboloide
Saber calcular las dimensiones del reflector no es imprescindible para utilizarlo, pero a algunas personas les puede resultar interesante. Así es como hice el cálculo:
La ecuación de una parábola se puede escribir como:
donde f es la distancia focal. En tres dimensiones, para un paraboloide, esto se convierte en:
Diferenciando obtenemos:
Si consideramos un "aro" estrecho de material que rodea el paraboloide perpendicular al eje y, con un ancho dr en la dirección r y dy en la dirección y, su ancho real es, según Pitágoras:
(SQR significa raíz cuadrada).
Esto se simplifica a:
Al poner la expresión para dy/dr, el ancho se convierte en:
La circunferencia del aro es 2.pi.r, por lo que el área total de material en el aro es:
Por tanto, la masa del aro es proporcional a ésta.
Por simetría, el centro de masa del aro debe estar en el eje y (eje de simetría) del paraboloide, por lo que el momento de su peso respecto al foco es proporcional a:
(El sentido de la resta no es importante para nuestro propósito).
Sustituyendo y, el momento es proporcional a:
Reordenando, esto se convierte en:
Como sólo nos interesa encontrar la condición cuando la suma de muchas de estas cantidades llega a cero, podemos ignorar todos los factores constantes distintos de cero. f es una constante y dr será una constante si consideramos un conjunto de aros de igual ancho. Entonces el momento del peso del aro es proporcional a:
Escribiendo k para 4f ^ 2, esto se convierte en simplemente:
Un programa de computadora para hacer el cálculo debe sumar una gran cantidad de expresiones como esta, para valores de r igualmente espaciados, comenzando desde cero. Inicialmente, cuando r^2 es menor que k, la expresión tiene un valor positivo y la suma se vuelve cada vez más positiva. Sin embargo, a medida que r aumenta, se alcanza un punto en el que r ^ 2 se vuelve mayor que k. A partir de ahí la expresión es negativa y la suma disminuye. Finalmente, la suma cruza cero y se vuelve negativa. El valor de r en este punto de cruce es lo que queremos encontrar.
Aquí está el programa que escribí para hacer todo el trabajo duro, escrito en QBasic:
La expresión para q, en el programa, es la misma que deduje arriba. El programa suma muchas de estas q para obtener un total, t, y se detiene cuando t se vuelve negativo. Luego, el programa realiza una interpolación en el aro final, lo que mejora enormemente la precisión, y luego calcula los valores de d y a e imprime las respuestas.
Los resultados que proporciona este programa fueron confirmados, con una precisión de diez dígitos significativos, por el Dr. Robert Israel, del Departamento de Matemáticas de la Universidad de Columbia Británica, Canadá. Hizo el cálculo de una manera muy diferente. El hecho de que su resultado y el mío coincidan confirma que ambos métodos son lógicamente correctos. Estoy en deuda con el Dr. Israel por esto.
Con diez dígitos significativos, la relación entre el radio del borde y la distancia focal es 2,718683325. La profundidad del plato, en unidades de distancia focal, es 1,847809755. El radio angular del borde, visto desde el foco, es 72,68013409 grados. Aproximadamente.
Envíeme un correo electrónico con cualquier pregunta:
williamsdavid65 en jeemale punto kom
DOwenWilliams 18:03, 3 de julio de 2010 (UTC) David Williams