Processor task scheduling using AI algorithms.
Task scheduling in fog computing[edit | edit source]
Fog computing brings cloud services to the network's edge. In such a case, it is vital to decide where applications should be implemented in order to meet their quality of service criteria. As a result, a cloud-fog system requires an efficient task scheduler to determine where applications should run. The problem is formulated as below:
Assign N tasks, each with a deadline, to M nodes, each with a price, in a way that we can process the maximum number of tasks before their deadline at the lowest possible cost.
In this project, I have implemented five different AI algorithms including:
- Greedy algorithm
- Hill climbing
- Random restart Hill climbing
- Simulated annealing
- Genetic algorithm
When you start the program, after selecting one of the methods listed above, you enter the number of tasks and nodes. Each task will then be given a random deadline (in seconds) and each node will be assigned a cost and a speed. The output will be:
- the efficiency of that algorithm ( based on number of tasks that were finished before their deadline)
- number of tasks that finished before their deadline
- number of tasks that finished after their deadline
- and the total cost
Finally, in case you want to see more information about the tasks and efficiency you can see an excel file created in the root directory of the program containing a table and a graph.

1. Greedy algorithm[edit | edit source]
In this approach, tasks and nodes are first sorted ascendingly based on their deadlines and costs respectively. Then, for each task in the list, we examine the sorted nodes and assign the task to the first node that can complete it before the deadline (it will be the cheapest node that can process the task). If none of the nodes can complete the task before its deadline, it will be stored in a queue, and after all other tasks have been completed, the tasks in the queue will be assigned to cheapest nodes.
2. Hill climbing algorithm[edit | edit source]
Hill climbing algorithm is a local search algorithm which continuously moves in the direction of increasing elevation/value to find the peak of the mountain or best solution to the problem. It terminates when it reaches a peak value where no neighbor has a higher value. It is also called greedy local search as it only looks to its good immediate neighbor state and not beyond that. In this program, the initial state is generated where each task will be assigned randomly to a node. Then the neighbors of the state will be generated where each task is assigned randomly to other nodes except the one in the current state. Each time, the value of the state will be evaluated, and we will stop generating the neighbors as soon as we reach a state that has a higher value than the current one. To avoid having redundant paths and getting stuck in a loop, we will keep track of changed tasks in each step. The algorithm stops when it can't find better values after generating 80 neighbors.
3. Random restart Hill climbing[edit | edit source]
Random-restart hill-climbing conducts a series of hill-climbing searches from randomly generated initial states, running each until it halts or makes no discernible progress. In this program you will enter the number of desired restarts of hill climbing and the result will be the one with the highest value.
4. Simulated annealing[edit | edit source]
A Simulated annealing algorithm is a method to solve bound-constrained and unconstrained optimization parameters models. The method is based on physical annealing and is used to minimize system energy. In every simulated annealing example, a random new point is generated. The distance between the current point and the new point has a basis of the probability distribution on the scale of the proportion of temperature. The algorithm aims at all those points that minimize the objective with certain constraints and probabilities. Those points that raise the objective are also accepted to explore all the possible solutions instead of concentrating only on local minima. In this program you will be able to enter the initial temperature and it will stop at T=0.1.
5. Genetic algorithm[edit | edit source]
A genetic algorithm is an adaptive heuristic search algorithm inspired by "Darwin's theory of evolution in Nature." It is used to solve optimization problems in machine learning. It is one of the important algorithms as it helps solve complex problems that would take a long time to solve. The evolution in this program begins with a population of 100 randomly generated individuals and is an iterative process, with the population in each iteration referred to as a generation. Every individual in the population's fitness is evaluated in each generation; the fitness value is based on the number of tasks completed before their deadline and the ultimate cost. The most fit individuals are chosen at random from the existing population, and their genomes are modified (recombined and sometimes randomly mutated) to generate a new generation. The new generation of potential solutions is then used in the algorithm's following iteration. The number of iteration will be set by user.
More pictures of line charts plotted by the app:
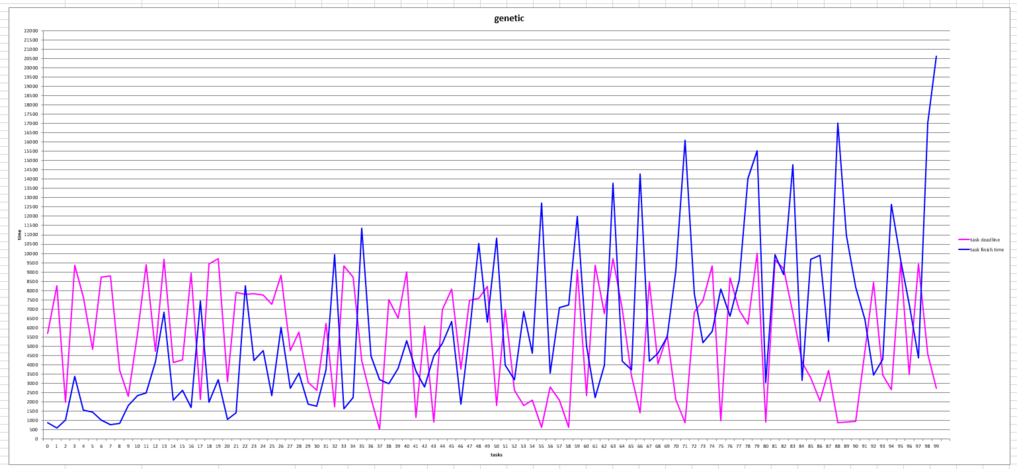
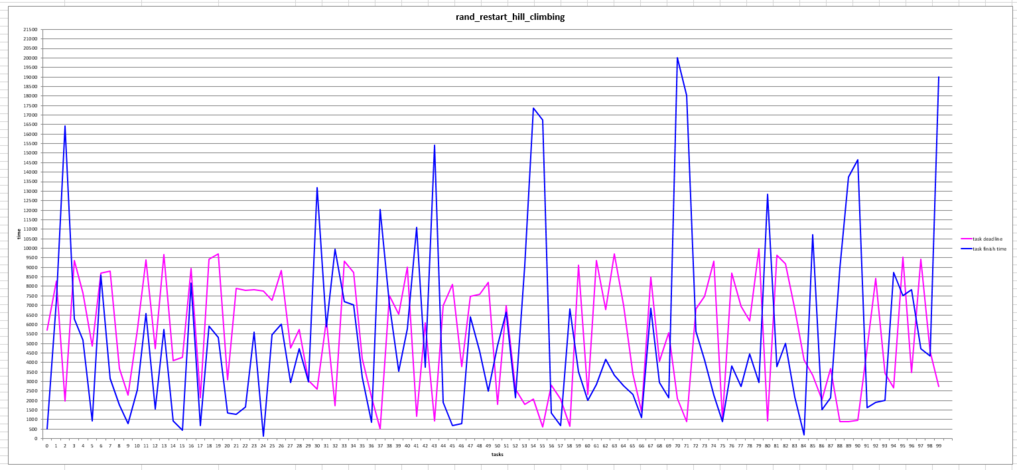
The codes of this projects is available at: