
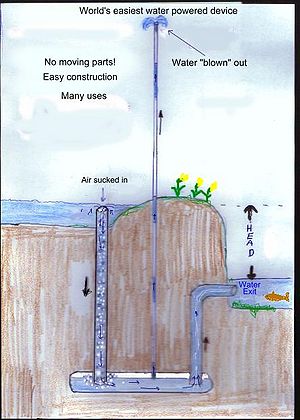
Die Pulspumpe ist ein einfaches, wasserbetriebenes mechanisches Gerät, das auch als Blasenpumpe bekannt ist. Komponenten dieser Pumpe werden für verschiedene Zwecke verwendet, darunter zur Ölförderung oder in Kühlkreisläufen. Wärmebetriebene Blasenpumpen sind am gebräuchlichsten, aber diese spezielle Konstruktion einer Pulspumpe, die die turbulente Strömung in einem Bach nutzt, um Luft einzufangen, ist noch nicht weit verbreitet. Die beiden Hauptvorteile dieser Pumpe sind, dass sie keine mechanischen oder beweglichen Teile hat und dass sie keine Chemikalien verwendet, sondern nur das Wasser aus einem Bach. Sobald sie in der Nähe eines Bachs installiert ist, kann die Pumpe Wasser nur mithilfe der Energie des Bachs heben.
Ich erteile die Erlaubnis, alle Bilder und animierten GIFs, die ich in der Vergangenheit für dieses Projekt erstellt habe, wiederzuverwenden und anzupassen. Brian White, 3. Mai 2010
Inhalt
Hintergrundinformation
Übersicht
Die Pulspumpe ist eine Kombination aus Trompe- und Lufthebepumpe . In der Nähe eines Bachs installiert, kann die Pulspumpe Wasser auf eine Höhe über dem Bachniveau pumpen. Dadurch können Bäche an schwer zugänglichen Stellen leicht erreicht werden oder Wasser aus einem Bach kann zu Bewässerungs- oder Trinkwasserzwecken an einen anderen Ort geleitet werden.
Die Pulspumpe verwendet einfach den Trompe-Teil, um den Airlift-Teil anzutreiben. Ein Video, in dem die Pumpe erklärt wird, finden Sie hier .
Vorteile
Wie im Abschnitt „Einführung“ erwähnt , hat die Pumpe zwei Hauptvorteile. Erstens hat diese Bauart der Pulspumpe keine chemischen Komponenten, wie sie bei wärmebetriebenen Blasenpumpen üblich sind, die nach ähnlichen Prinzipien arbeiten (siehe unten „Wärmebetriebene Blasenpumpen“). Dadurch kann die Pumpe für eine Vielzahl von Aufgaben eingesetzt werden, bei denen nicht verunreinigtes Wasser gepumpt werden muss, wie etwa Bewässerung und zum Pumpen von Trinkwasser. Da keine Chemikalien erforderlich sind und das verfügbare Flusswasser als Pumpflüssigkeit verwendet wird, werden die Kosten der Pumpe außerdem erheblich gesenkt.
Zweitens hat die Pulspumpe keine beweglichen Teile. Nach der Installation nutzt diese Pumpe die turbulente Strömung des Wassers, um Luft einzufangen, und die Schwerkraft, um sie zu komprimieren (siehe Abschnitt „Funktionsprinzip“ weiter unten), um einen Teil des Wassers auf eine Höhe über der des Wassers zu pumpen. Es sind keine mechanischen Teile erforderlich, die normalerweise teurer und schwieriger zu installieren sind.
Zusätzlich zu diesen Vorteilen wird auch behauptet, dass Pulspumpen einen positiven Effekt auf die Wasserqualität haben, indem sie den Sauerstoffgehalt erhöhen. [1] Die Grundidee besteht darin, dass durch das Mischen von Luft und Wasser in der Ansaugpumpe die vergrößerte Oberfläche zwischen ihnen es ermöglicht, mehr Sauerstoff ins Wasser zu übertragen, als dies normalerweise in einem Bach der Fall ist. Weitere Forschungen müssen durchgeführt werden, um diese Idee zu bestätigen.
Geschichte
Trompen wurden schon vor der Erfindung von Wasserturbinen eingesetzt , um Luft in Minen zu pumpen, um die pneumatischen Maschinen, mit denen einige der ersten Alpentunnel gebaut wurden, mit Luft zu versorgen und um Motoren anzutreiben, die im späten 19. Jahrhundert die wohlhabenden Viertel von Paris beleuchteten. Lufthebepumpen werden von Wasserversorgern noch immer häufig eingesetzt, um Wasser aus sehr tiefen Brunnen zu pumpen. Sie verwenden Kompressoren, um Luft in die Brunnen zu drücken, und die Luft strömt durch ein zweites, breiteres Rohr, das Wasser mit sich führt.
Funktionsprinzip
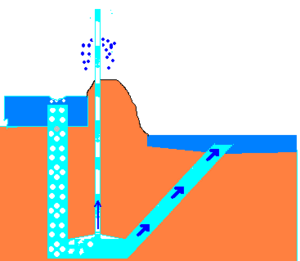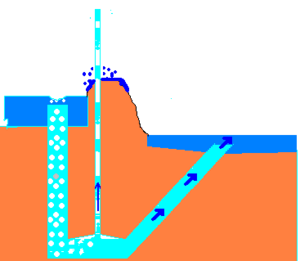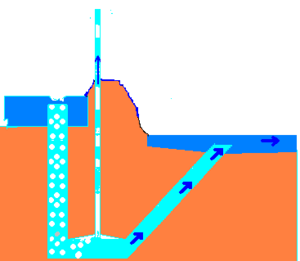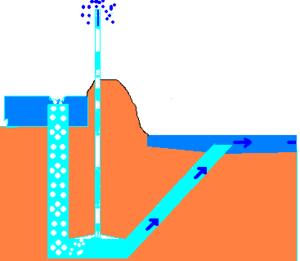
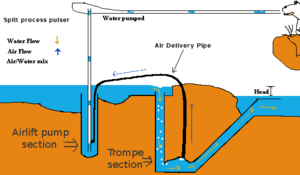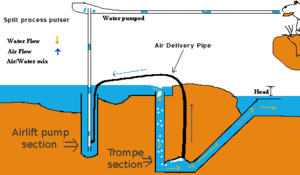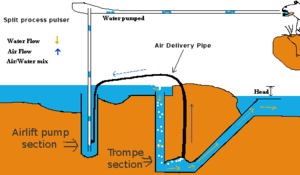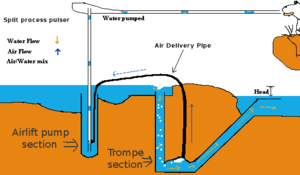

Eine Pulspumpe (auch Blasenpumpe genannt) verwendet einen hydraulischen Wasserdruck, um Luft zu komprimieren, die das Wasser verdrängt und Wasser „pulsierend“ auf eine höhere Höhe als zuvor drückt. Dies funktioniert nach dem gleichen Prinzip wie eine Trompe- und eine Lufthebepumpe.
Konstruktion eines Modells
Basierend auf dem Erfolg anderer ähnlicher Pilotprojekte [2] wurde ein Proof-of-Concept-Modell konstruiert. Die hier aufgeführten Materialien dienen zum Bau eines Modells, das für Anwendungen im kleinen Maßstab, wie sie im Abschnitt „Vorhandene Pumpen“ weiter unten beschrieben werden, oder für weitere Tests verwendet werden kann. Bei den hier beschriebenen Kunststoffrohren handelt es sich um flexible Kunststoffrohre, die für Tests nützlich sind, da sie auf die richtige Höhe gebogen und für verschiedene Tests wiederverwendet werden können. Es könnten jedoch auch feste PVC-Rohre verwendet werden, die in einer Nicht-Testsituation praktischer zu implementieren wären. (Siehe Abschnitt „ Testen“ )
Materialien
Diese Materialien sind fester Bestandteil der Pulspumpe dieses Modells. Außer einer Schere zum Schneiden der Schläuche wurden keine weiteren Werkzeuge verwendet.
Abb. 1: 2 Stücke transparenter Kunststoffschlauch mit 3/4 Zoll Innendurchmesser
Abb. 1a: 1 Stück transparenter Kunststoffschlauch mit 3/8 Zoll Innendurchmesser
Abb. 1b: 2 x 3/4 Zoll Kunststoffschlauchverbinder, die an einem Ende in den Kunststoffschlauch passen und am anderen Ende ein Gewinde haben
Abb. 1c: 1 @ 3/8"-Kompressionsverschraubung, die an einem Ende um das Rohr passt, es an Ort und Stelle drückt und am anderen Ende ein Gewinde hat
Abb. 1d: 1 @ 1 1/2" Dreiwegeverbinder mit zwei gegenüberliegenden Reibschlussöffnungen und einer darüber
Abb. 1e: 2 @ 1 1/2" bis 3/4"-Anschlüsse, an einem Ende innen mit Gewinde versehen und an einem Ende reibungsschlüssig verbunden, um den Dreiwegeanschluss und den Kunststoffrohranschluss anzuschließen
Abb. 1f: 1 @ 1 1/2" bis 3/8"-Anschluss, an einem Ende innen mit Gewinde versehen und an einem Ende mit Reibungspassung zum Anschluss an den Dreiwegeanschluss und den Kunststoffrohranschluss
Zusätzlich zu den oben genannten Artikeln wurden diese zusätzlichen Materialien benötigt, um dieses Modell einzurichten und zu testen:
Abb. 1: 1 Schlauch zur kontrollierten Wasserzufuhr
Abb. 1a: Stützen und Verbindungsmechanismen zur Befestigung von Rohren
Abb. 1b: Eimer und Spüle zum Ablassen von überschüssigem Wasser
Kosten
Die Kosten für diesen Prototyp waren relativ hoch, aber verglichen mit den Kosten der meisten anderen Wasserpumpen sind sie sehr niedrig. Außerdem ist es wahrscheinlich, dass dieser Entwurf, wenn er in größerem Maßstab gebaut wird, zu wesentlich geringeren Kosten gebaut werden kann. Die Kosten für diesen Prototyp sind unten ungefähr angegeben:
| Artikel | Preis |
| Kunststoffschläuche | $40 |
| Schlauchverbinder (alle) | $10 |
| Dreiwege-Stecker | $10 |
| Gesamt | 60 $ |
Erstellen und Einrichten des Modells
Der Aufbau dieses Modells ist sehr unkompliziert, da es nur wenige Komponenten hat. Der schwierige Teil besteht darin, die Rohre so einzurichten, dass sie so vertikal wie möglich bleiben.
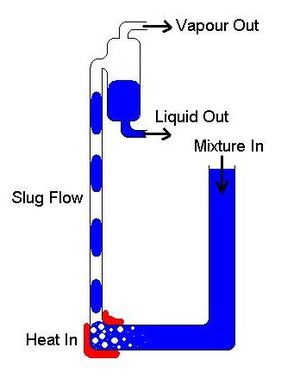
Unten sehen Sie ein Video des Modells, das ich während der Arbeit erstellt habe. Beachten Sie die Blasen in den Rohren, die deutlich zeigen, dass sich das Einlassrohr im Blasenströmungsregime und das Pumprohr im Schwallströmungsregime befindet.
Der zum Erstellen dieses Modells verwendete Prozess wird unten ausführlich beschrieben.
- Zunächst müssen die Rohre auf die gewünschte Länge zugeschnitten werden.
- Bei diesem Modell wurde das 3/4-Zoll-Zulaufrohr auf eine Länge von ca. 2,1 m zugeschnitten.
- Das Auslassrohr wurde ebenfalls auf eine Länge von 2,1 m zugeschnitten, sodass es für verschiedene Tests variiert werden kann.
- Der Pumpschlauch wurde lang gehalten, um bei den nachfolgend beschriebenen Versuchen die Höhe variieren zu können.
- Bei dieser Ausführung dient der Dreiwegeverbinder als Trennbehälter für die Pulsierpumpe.
- Die 1 1/2" bis 3/4"-Anschlüsse passten genau in die direkt gegenüberliegenden Seiten des Dreiwegeverbinders. Um einen dichten Sitz zu gewährleisten, kann Epoxidharz aufgetragen werden.
- Der 1 1/2" bis 3/8"-Stecker wurde in das Dreiwege-Steckerloch gepasst, das 90 Grad von den beiden anderen Löchern entfernt ist.
- Zuerst wird die Klemmverschraubung für den 3/8"-Anschluss an den 1 1/2" auf 3/8"-Anschluss geschraubt
- Anschließend schrauben Sie die Kunststoff-Rohrverschraubungen für den 3/4"-Anschluss an die 1 1/2" bis 3/4"-Anschlüsse an
- Durch Verbinden dieser Teile vor dem Anschließen der Schläuche wird ein Verheddern der Schläuche vermieden.
- Der 3/4-Zoll-Schlauch sollte fest über den 3/4-Zoll-Anschluss passen. Er kann zusätzlich an Ort und Stelle gehalten werden, indem man eine Metallklemme darum festzieht.
- Die 3/8-Zoll-Kompression hat eine Komponente, die um die Außenseite des Schlauchs geht, ein kleines Stück passt in den Schlauch, um ihn offen zu halten, dann kann das Stück, das um die Außenseite des Schlauchs liegt, in die Kompressionsverschraubung geschraubt werden, die bereits mit dem 1 1/2-Zoll-auf-3/8-Zoll-Anschluss verbunden ist, und hält den Schlauch an Ort und Stelle.
- Nun sind alle Hauptkomponenten der Pumpe angeschlossen. Der nächste Schritt besteht darin, die Pumpe einzurichten.
- Bestimmen Sie zunächst eine Methode, mit der die Rohre an ihrem Platz gehalten werden. Hierzu kann ein Holzbrett verwendet und die Rohre daran genagelt werden. Um ein leicht anpassbares Gerät zu erhalten, wurden die Rohre in diesem Experiment mit Klebeband am Trägersystem und an der Wand befestigt.
- Stellen Sie sicher, dass die Rohre vertikal sind und dass die Höhe der Rohre den gewünschten Wert hat.
- Ein Schlauch wurde an der Oberseite des Einlassrohrs angeschlossen, indem sowohl das Rohr mit 3/4" Durchmesser als auch die Schlauchdüse in ein kurzes Abfallrohr mit 1" Durchmesser eingeführt wurden. Der Schlauch wurde verwendet, um die Strömung des Stroms zu simulieren.
- Der Abflussschlauch war so eingestellt, dass er in die Spüle ablief.
Testen
Nach dem Aufbau des Modells wurden einige Vorversuche durchgeführt, um zu zeigen, dass die Pumpe tatsächlich nützliche Arbeit leisten kann. Bevor diese Bauart einer Pulspumpe breitere Akzeptanz und Verwendung findet, sind noch viel ausführlichere Tests erforderlich.
Bei diesem Test wurden zwei Variablen geändert, die hydraulische Förderhöhe der Pumpe und die Höhe des Pumpenschlauchs.
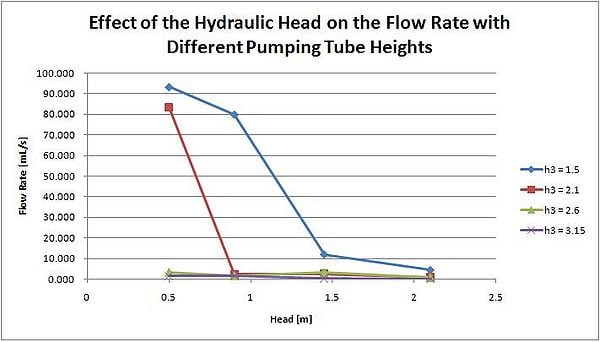
Es wird erwartet, dass mit zunehmender hydraulischer Förderhöhe auch die Durchflussrate zunimmt. Dieser Effekt wurde von der Pumpe nachgewiesen und die Ergebnisse sind unten dargestellt.
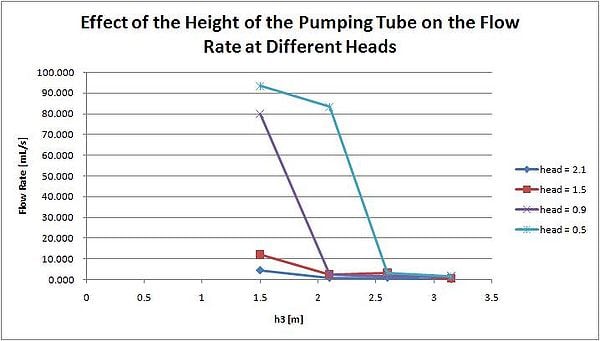
Mit zunehmender Höhe des Pumprohrs ist mehr Energie erforderlich, damit die Impulse die Oberseite des Rohrs erreichen. Die entsprechende Abnahme der erwarteten Durchflussrate ist unten zu sehen.
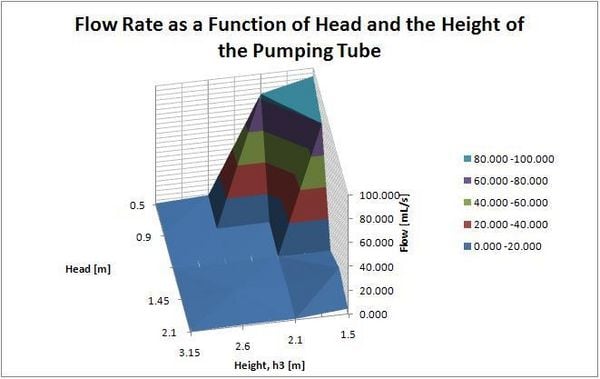
Wenn die Auswirkungen dieser beiden Variablen kombiniert werden, ergibt sich ein Diagramm, das zeigt, wie die Durchflussrate sowohl von der hydraulischen Druckhöhe als auch von der Höhe des Pumpenrohrs abhängt. Dieses Diagramm kann verwendet werden, um die Beziehung zwischen diesen beiden Größen und der Durchflussrate zu veranschaulichen. Selbst bei großen hydraulischen Druckhöhen kann die Durchflussrate gering sein, wenn die Höhe des Pumpenrohrs groß ist. Darüber hinaus verringert eine kleine Druckhöhe die durch das Pumpenrohr gepumpte Wassermenge, selbst wenn die Höhe des Pumpenrohrs gering ist. Dies wird unten gezeigt.
Bei Spitzenleistung (große Förderhöhe und kurzes Pumpenrohr) pumpte dieses Modell mit einer Geschwindigkeit von fast 100 ml/s oder 1 Liter alle 10 Sekunden! Trotz mehrerer Tests bei jedem Wert ist die Reproduzierbarkeit dieser Ergebnisse immer noch fraglich. Unabhängig von der genauen Durchflussrate zeigt dieses Experiment, dass die Pulspumpe ein enormes Potenzial für den weit verbreiteten Einsatz zum Pumpen von Wasser hat. Weitere Tests sollten durchgeführt werden, um die genaue Beziehung zwischen Durchfluss, Förderhöhe und Höhe des Pumpenrohrs besser bewerten zu können.
Wissenschaftliches Modell
Obwohl es Pulspumpen oder zumindest verschiedene ähnliche Ausführungen dieser Art von Pumpen schon seit geraumer Zeit gibt, gibt es keine gute Erklärung oder Modell, das sie beschreibt. Ähnliche Probleme, wie bei wärmebetriebenen Blasenpumpen , sind oft geschlossene Systeme, die kein Auslassrohr benötigen. In diesem Abschnitt werden einige der wissenschaftlichen Prinzipien hinter der Funktionsweise dieser Pumpe vorgestellt und zwei verschiedene Modelle entwickelt. Das erste Modell ist das einfache Manometermodell und das zweite ist das kompliziertere Druckmodell .
Zweiphasenströmung
Ein wichtiges Konzept für diese Konstruktion ist die Zweiphasenströmung , d. h. wenn eine Flüssigkeit und ein Gas durch einen Meniskus getrennt sind. Es gibt mindestens sieben verschiedene Arten der Zweiphasenströmung, [3] von denen mehrere während des Betriebs der Pulspumpe auftreten.
Schwallströmung
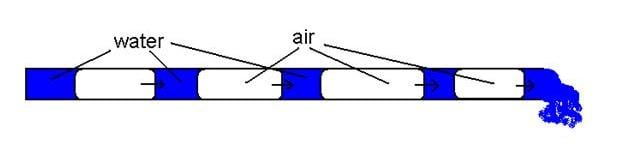
Die Hebewirkung der Pumpe im Pumpenrohr erfolgt hauptsächlich im Schwallströmungsregime. Bei der Schwallströmung trennen sich Flüssigkeit und Gas in verschiedene Schichten, die fast den gesamten Querschnitt des Rohrs einnehmen, wie unten dargestellt.
Bei Strömungen im Pfropfenregime hängt der zulässige Rohrdurchmesser von der Strömungsgeschwindigkeit und der Viskosität ab. Die Geschwindigkeit im Pumpenrohr ist selbst mit einigen vereinfachenden Annahmen sehr schwer zu beschreiben. Wenn das Rohr beispielsweise nicht vertikal ist, sind die Blasen nicht mehr symmetrisch, was zu Änderungen der Blasengeschwindigkeit führt. Mehrere dimensionslose Terme, darunter die Froude-Zahl, die Eötvös-Zahl und die Reynolds-Zahl, sind erforderlich, um die Strömung vollständig zu beschreiben. [4] Obwohl noch keine klare Einigung über das am besten geeignete Modell besteht, wurden mehrere vorgeschlagen. [5]
Die vollständige Bestimmung der Fluideigenschaften während der Schwallströmung und die Ableitung eines Modells, das alle Auswirkungen dieses Strömungsregimes umfasst, liegen außerhalb des Rahmens dieses Modells. Stattdessen wird ein viel einfacheres Modell betrachtet, das vollständig vertikale Rohre und eine gleichmäßige Strömung usw. annimmt, wie weiter unten erläutert.
Manometer-Modell
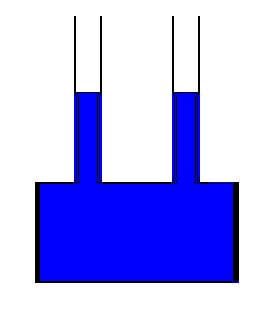
Bei mehreren Röhrchen in der gleichen Flüssigkeit ist die maximale Höhe der Flüssigkeit in jedem Röhrchen durch die Massenerhaltung gegeben. Nach dem gleichen Prinzip wie bei einem Manometer bestimmen Außendruck, Dichte und Durchmesser des Röhrchens die Höhe der Flüssigkeit. Das bedeutet, dass die Dichte ρ mal Querschnittsfläche des Röhrchens A mal Höhe der Flüssigkeit h für jedes Röhrchen gleich ist, wenn sie mit dem gleichen Druck austreten, wie in dem Diagramm rechts gezeigt. Das bedeutet, dass, wenn ein geschlossener Behälter mit Wasser gefüllt ist und oben zwei gleiche Strohhalme stecken, die zur Luft hin offen sind, die Flüssigkeit in den Strohhalmen auf die gleiche Höhe steigt, d. h. es wird nicht mehr Flüssigkeit in einem Strohhalm sein als in dem anderen.
Das heißt:
(RAH)1=(RAH)2{\displaystyle \ (\rho Ah)_{1}=(\rho Ah)_{2}}
Dies ist sinnvoll, wenn alle Variablen konstant sind. Bei einer Pulspumpe ist das Problem komplizierter. Es gibt ein Einlassrohr und ein Auslassrohr mit gleichem Querschnitt, aber unterschiedlicher Höhe, und dann gibt es das Pumprohr mit kleinerer Fläche und größerer Höhe. Die Einlass- und Auslassrohre sind fast vollständig mit Wasser gefüllt, sodass die Dichte annähernd der von Wasser entspricht. Zu einem bestimmten Zeitpunkt ist jedoch ein großer Teil des Pumprohrs mit Luft und nicht mit Wasser gefüllt. Die obige Gleichung lautet dann:
RInATEs istR(AH)ichNmEs istT=RInATEs istR(AH)ÖInTmEs istT+[RInATEs istR%InATEs istR+RAichR%AichR](AH)PInMP{\displaystyle \ \rho _{Wasser}(Ah)_{Einlass}=\rho _{Wasser}(Ah)_{Auslass}+[\rho _{Wasser}\%_{Wasser}+\rho _{Luft}\%_{Luft}](Ah)_{Pumpe}}
Oder, wenn Zulauf- und Ablaufrohr den gleichen Querschnitt haben:
RInATEs istRA(HichNmEs istT−HÖInTmEs istT)=[RInATEs istR%InATEs istR+RAichR%AichR](AH)PInMP{\displaystyle \ \rho _{Wasser}A(h_{Einlass}-h_{Auslass})=[\rho _{Wasser}\%_{Wasser}+\rho _{Luft}\%_{Luft}](Ah)_{Pumpe}}
WoHichNmEs istT−HÖInTmEs istT{\displaystyle h_{Einlass}-h_{Auslass}}
HPInMP=RInATEs istRA(HichNmEs istT−HÖInTmEs istT)[RInATEs istR%InATEs istR+RAichR%AichR]APInMP{\displaystyle h_{Pumpe}={\frac {\rho _{Wasser}A(h_{Einlass}-h_{Auslass})}{[\rho _{Wasser}\%_{Wasser}+\rho _{Luft}\%_{Luft}]A_{Pumpe}}}}
Das Hauptproblem bei diesem Modell ist, dass es die Geschwindigkeit der Flüssigkeit beim Durchlaufen der Pumpe ignoriert. Dies ist eine nicht zu vernachlässigende Größe, denn wenn die Bewegung der Flüssigkeit vernachlässigbar wäre, würde sich die Luft im Auslassrohr vom Wasser trennen und die Pumpe würde ihre Fähigkeit verlieren, Wasser zu bewegen. Dieses Manometermodell veranschaulicht jedoch das Grundprinzip der Pumpe und widerlegt die häufigste Kritik an der Pulspumpe, nämlich, dass es physikalisch unmöglich ist, dass das kleinere Pumpenrohr Wasser über die anfängliche Höhe des Stroms hinaus pumpt. Das obige Argument zeigt, dass dies nur zutrifft, wenn die Flüssigkeit im Pumpenrohr stationär ist oder die vorhandene Luftmenge vernachlässigbar ist.
Druckmodell
Theorie
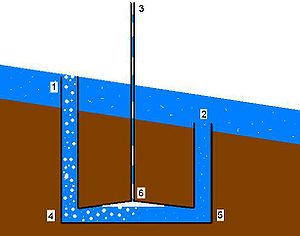
Um die Geschwindigkeit zu berücksichtigen, muss die Strömung detaillierter ausgewertet werden, wobei die Energieerhaltung und die Bernoulli-Gleichung verwendet werden . Diese Methode modelliert die Druckänderung der Strömung an den verschiedenen Punkten
An Stelle 4 ist der Druck von Stelle 1 gegeben durch:
P4=P1+R4GH1−R4(In42−In12)2{\displaystyle \ P_{4}=P_{1}+\rho _{4}gh_{1}-{\frac {\rho _{4}(v_{4}^{2}-v_{1}^{2})}{2}}}
Ebenso bei 5 aus 2:
P5=P2+R5GH2−R5(In52−In22)2{\displaystyle \ P_{5}=P_{2}+\rho _{5}gh_{2}-{\frac {\rho _{5}(v_{5}^{2}-v_{2}^{2})}{2}}}
Und bei 6 von 3:
P6=P3+R6GH3−R6(In62−In32)2{\displaystyle \ P_{6}=P_{3}+\rho _{6}gh_{3}-{\frac {\rho _{6}(v_{6}^{2}-v_{3}^{2})}{2}}}
Die Geschwindigkeit bei 3 wird als Null angenommen, um die maximale Höhe zu bestimmen, bis zu der das Wasser gepumpt werden kann. Dies gibt eine Obergrenze für die Höhe vor, die das Wasser erreichen kann. Außerdem kann angenommen werden, dass der Druck bei 1, 2 und 3 ungefähr eine Atmosphäre beträgt, da „3“ in die Atmosphäre austritt und „1“ und „2“ nur einen sehr geringen hydrostatischen Druck haben, der mit der Tiefe des Stroms zusammenhängt. Wenn man eine Kontrollvolumenanalyse am unteren Behälter zwischen 4, 5 und 6 durchführt, ergibt sich aus der Massenerhaltung:
R4A4In4=R5A5In5+R6A6In6{\displaystyle \\rho_{4}A_{4}v_{4}=\rho_{5}A_{5}v_{5}+\rho_{6}A_{6}v_{6}}
Die Flächen aller Rohre sind aus der Geometrie des Experiments bekannt. Das Auslassrohr hat einen minimalen Luftgehalt, daher kann angenommen werden, dass die Dichte der von Wasser entspricht.
Aufbauend auf den Arbeiten einer Quelle [6] , die eine wärmebetriebene Blasenpumpe in einem geschlossenen System analysierte, kann die Druckänderung von 4 und 5 auf 6 wie folgt beschrieben werden:
P6=P4−R6In4(In6−In4)−P5+R6In5(In6−In5){\displaystyle \ P_{6}=P_{4}-\rho _{6}v_{4}(v_{6}-v_{4})-P_{5}+\rho _{6}v_{5 }(v_{6}-v_{5})}
Bis zu diesem Punkt der Herleitung wurden alle Annahmen für einen ziemlich allgemeinen Fall getroffen. Die folgenden Annahmen im Modell liefern ein spezifischeres, vereinfachtes Modell. Die erste Annahme ist, dass die Geschwindigkeit zwischen 4 und 5 ungefähr konstant ist. Da nur ein kleiner Teil der Flüssigkeit umgeleitet wird, um aus dem Pumpenrohr auszutreten, wird angenommen, dass der Großteil der Flüssigkeit seinen Impuls beibehält, während sie weiter durch das Auslassrohr fließt.
Zweitens wird angenommen, dass der Gasgehalt im Pfropfenregime innerhalb des Pumprohrs 70 % beträgt, was ein Durchschnittswert für den Pfropfenfluss ist. Außerdem wird angenommen, dass sich das Gas im Einlassrohr im Blasenströmungsregime befindet, wo der Gasgehalt im Durchschnitt 30 % beträgt. [7] Dies bedeutet, dass:
R6=0,7RAichR+0,3RInATEs istR{\displaystyle \ \rho _{6}=0.7\rho _{Luft}+0.3\rho _{Wasser}}
R4=0,3RAichR+0,7RInATEs istR{\displaystyle \ \rho _{4}=0.3\rho _{Luft}+0.7\rho _{Wasser}}
Testen der Theorie
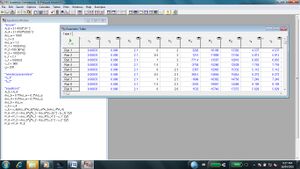
Mit diesen sieben Gleichungen und den dazugehörigen Annahmen hat das Druckmodell immer noch eine Unbekannte mehr als die Gleichung, was bedeutet, dass eine angemessene Höhe durch Iteration bestimmt werden muss. Die Eingaben sind die geometrischen Parameter des Systems, und der Druck und die Geschwindigkeit bei „4“, wo der höchste Druck erwartet wird, sollten ausgegeben werden. Wenn diese Werte angemessen sind, kann das System so eingerichtet werden, dass es funktioniert; wenn nicht, sollte eine weitere Iteration durchgeführt werden.
Ein erster Versuch zur Modellierung dieses Systems wurde mithilfe der EES-Software durchgeführt. Die obigen Gleichungen wurden definiert und einige Anfangsbedingungen festgelegt. Wie im Bild zu sehen ist, müssen zusätzlich zu den oben aufgeführten Annahmen die Höhe und der Durchmesser der Rohre sowie die Geschwindigkeit des Stroms bei 1 und 2 eingegeben werden. Das Programm gibt dann die Geschwindigkeit im gesamten Rohr und die Drücke aus. Um die Gültigkeit dieses Modells besser beurteilen zu können, kann dieses oder ein ähnliches EES-Programm verwendet werden.
Vorhandene Pulserpumpen
Pulspumpen haben keine Glaubwürdigkeit, da es keine Peer-Reviews gibt, obwohl sie nun weiter erforscht werden (siehe die externen Links unten). Es wurden jedoch mehrere Modelle gebaut, und es sind online Videos verfügbar, die zeigen, wie sie funktionieren und wie sie funktionieren. Dieses Design der Pulspumpen ist nicht patentiert und die Designs sind gemeinfrei. [8]
Funktionierende Pulspumpe
Ein Beispiel für eine 20 Jahre alte, funktionierende Pulspumpe ist hier verfügbar , sofern sie nicht zu wenig belastet. Diese Pumpe wird von einem kleinen Bach angetrieben, der 300 Liter Wasser aus einer Höhe von 0,5 Metern fördert und so die Energie erzeugt. Die Zahlen dieser Pumpe zeigen, dass eine scheinbare Wassergeschwindigkeit im Trompetenabschnitt zwischen 0,32 und 0,68 Metern pro Sekunde schnell genug ist, um die Luftblasen durch das Rohr zu befördern.
Die scheinbare Luftgeschwindigkeit im Lufthebeabschnitt scheint zwischen 0,7 ms-1 und 1,5 Metern pro Sekunde am besten zu funktionieren. Dies geschah bei Verwendung von 12 mm- und 19 mm-Rohren und geradem Pumpen nach oben.
Eine niedrigere scheinbare Luftgeschwindigkeit funktionierte am besten beim Pumpen auf einer Steigung. (Die scheinbare Geschwindigkeit ist die Geschwindigkeit des Wassers oder der Luft durch die Rohre, vorausgesetzt, dass sich nur eine Flüssigkeit im Rohr befand.) Es ist ein guter Anhaltspunkt, wenn Sie Ihren eigenen Anhaltspunkt erstellen. Brian
Pulspumpen können laut Gaiatechnician mit viel größeren Durchflussmengen und Druckhöhen arbeiten .
Aufgrund ihrer extremen Einfachheit können sie für Gemeinden am Wasser von großem Wert sein. Die winzige Pulspumpe im Video kann etwa 5 Tonnen Wasser pro Tag in einen Vorratsbehälter pumpen. [9]
In einem zweiten Beispiel ( hier gezeigt ) wird die Pulspumpe zur Wasserversorgung von Tieren verwendet. Sie hat eine Zufuhrmenge von ungefähr 30 Litern/min durch ein 40 mm großes Abflussrohr. Sie kann 30 ml/min auf 3 m oder 1 l/min auf 1 m heben. [10]


Mike Donevan von Practical Farm Ideas hat mir im Austausch gegen einen Link gestattet, Bilder und Texte aus der Zeit zu verwenden, als die Pumpe in seinem Magazin erschien. http://www.farmideas.co.uk/
Ich denke, sie werden für jeden wertvoll sein, der ungefähre Zahlen zur Einschätzung guter Rohrgrößen für seine Projekte sucht.
Brian weiß
Wärmebetriebene Blasenpumpen
Wärmebetriebene Blasenpumpen sind die am häufigsten vorkommende Art von Pulspumpen. Sie verwenden ein ähnliches Funktionsprinzip wie diese Pulspumpenkonstruktion, jedoch in einem geschlossenen System. Im Allgemeinen wird ein Kühlmittel mit einem Siedepunkt unter dem von Wasser mit der Flüssigkeit vermischt. Nachdem die Mischung komprimiert wurde, wird sie erhitzt, wodurch sich aus dem Kühlmittel in der Arbeitsflüssigkeit Blasen bilden. Die Kühlmittelblasen drücken dann das Wasser in das Pumpenrohr, wie bei der Pulspumpe. Die Mischung gelangt dann in eine Trennkammer, wo die Flüssigkeit zu einem Absorber und das Kühlmittel zu einem Kondensator geleitet wird. [11]
Schlussfolgerungen
Dieses spezielle Design einer Pulspumpe ist extrem einfach zu bauen und hat das Potenzial, die Art und Weise, wie Wasser gepumpt wird, erheblich zu verändern. Es werden keine Chemikalien zum Pumpen des Wassers verwendet, sodass das in den Bach zurückgeleitete Wasser nicht verunreinigt ist. Im Gegenteil, es gibt Behauptungen, dass das in den Bach zurückgeleitete Wasser mehr Sauerstoff enthält und so eine bessere Umgebung für Unterwasserlebewesen bietet. Das Wasser, das nicht in den Bach zurückgeleitet wird, kann zur Bewässerung von Land oder zur Trinkwassergewinnung verwendet werden. Die zusätzliche Höhe, die die Pumpe bietet, ermöglicht es, Wasser weiter zu transportieren, als der Bach allein es bewegen könnte.
Die Pumpe selbst besteht aus sehr wenigen Materialien, nur einfachen Schläuchen und Verbindungen, und wenn ein optimales Design gefunden ist, kann sie kostengünstig hergestellt werden. Sobald die Pumpe einmal installiert ist, ist fast keine Wartung erforderlich. Abgesehen von den anfänglichen Installations- und Gerätekosten kann die Pumpe also die Menschen in der Nähe kostengünstig und einfach mit Wasser versorgen.
In dieser Analyse wurden sowohl ein experimentelles als auch ein theoretisches Modell entwickelt. Das experimentelle Modell basierte auf einem früheren Entwurf und diente als Machbarkeitsnachweis. Das Modell zeigte deutlich die erwarteten Trends und zeigte höchste Durchflussraten für einen großen hydraulischen Druck und ein kurzes Pumpenrohr. Es wurden zwei theoretische Modelle vorgeschlagen, von denen das erste auf dem Prinzip der Massenerhaltung basierte, wie ein Manometer. Dieses Modell lieferte eine grobe Schätzung der Höhe des zweiten Rohrs, die Gültigkeit ist jedoch sehr begrenzt, da es eine vernachlässigbare Geschwindigkeit annimmt. Es dient jedoch dazu, die Vorstellung zu widerlegen, dass dieser Entwurf für eine Pulspumpe physikalisch unmöglich ist. Das zweite theoretische Modell verwendete sowohl die Massenerhaltung als auch die Energieerhaltung, um die Geschwindigkeiten und Drücke in jeder Stufe der Pumpe zu bewerten. Dieses zweite Modell erfordert, dass der Benutzer die erzeugten Werte iteriert, um eine angemessene Geometrie unter bestimmten Bedingungen zu bestimmen. Mithilfe des Engineering Equation Solver wurde eine Vorlage erstellt, die es dem Benutzer ermöglicht, die getroffenen Annahmen zu iterieren, um die optimale Geometrie zu bestimmen.
Empfehlungen
Sowohl das experimentelle als auch das theoretische Modell würden von einem Peer Review und weiterer Forschung stark profitieren. Das experimentelle Modell sollte mit einem strengeren Testschema getestet werden, mit vielen weiteren Tests bei jeder Höhe und jedem Druck. Andere Variablen wie die Größe des Behälters, der Durchmesser der Rohre und die Strömungsgeschwindigkeit sollten ebenfalls getestet werden, um ihre Auswirkungen auf die Pulspumpe zu bestimmen, und es sollte ein breiterer Wertebereich verwendet werden. Das größte Problem bei diesem Experiment war ein Leck im Originalbehälter und -schlauch. Mit den oben beschriebenen Methoden können diese Probleme leicht überwunden werden und es bleibt mehr Zeit für die Durchführung detaillierterer Tests.
The theoretical model proposed could be further expanded and tested using software such as the EES program described above. In addition, there are several factors that were not accounted for that must be included in the model for it to accurately predict the flow rate through the pump. These include:
- Analysis of two phase slug flow in pumping tube
- Determination of air content and flow regime in inlet and outlet tubes
- Friction/Viscous losses
- Turbulent Flow
- Pressure gradient across separation container
External links
- Gaiatechnician's explaination on YouTube can be found here. For a more detailed explaination, visit his website
- Other videos of working pulser pumps can be found here and here
- Bubble Action Pumps Ltd. make a similar product, that pumps water through solar thermal panels. Check it out on their website.
- Altenergymag describes pulser pumps here
- All About Pumps also have a description here
- For a description of how to make a pulser pump, visit Instructables
References
- ↑ All About Pumps. Available at: http://web.archive.org/web/20210125002710/http://www.animatedsoftware.com/pumpglos/glpulser.htm [Accessed April 15, 2010].
- ↑ Brian White "Pulser Pumps" Available Online: http://nxtwave.tripod.com/gaiatech/pulser/builder.htm [Accessed April 3, 2010]
- ↑ J. B. McQuillen, R. Vernon and A. E. Dukler. "Flow regimes in gas-liquid flows" Available Online at: http://web.archive.org/web/20170704025739/http://www3.nd.edu/~mjm/flow.regimes.html [Accessed April 15, 2010]
- ↑ J. Fabre and A. Line "Modeling of Two-Phase Slug Flow" Annu. Rev. Fluid Mech: 1992. Available Online: http://arjournals.annualreviews.org/doi/pdf/10.1146/annurev.fl.24.010192.000321?cookieSet=1 [Accessed April 15, 2009]
- ↑ XIA Guo-dong, CUI Zhen-zhen, LIU Qing, ZHOU Fang-de, HU Ming-sheng "A Model for Liquid Slug Length Distribution in Vertical Gas-Liquid Slug Flow" Journal of Hydrodynamics: 2009. Available Online: [Accessed April 15, 2010]
- ↑ Susan J. White. "Bubble Pump Design and Performance" Georgia Institute of Technology: August 2001. Available Online at: http://www.me.gatech.edu/energy/SusanThesis.pdf [Accessed April 13, 2010].
- ↑ Micro Motion White Paper. "Explaining how two-phase flow affects mass flowmeters" Micro Motion, Inc. USA: 2004. Available online: http://web.archive.org/web/20130123193851/http://www.documentation.emersonprocess.com:80/groups/public_public_mmisami/documents/whitepaper/wp-00698.pdf [Accessed: April 15, 2010]
- ↑ Brian White „The Pulser Pump“. Verfügbar unter: http://www.altenergymag.com/emagazine.php?issue_number=03.10.01&article=pulser [Zugriff am 15. April 2010].
- ↑ Pulser Pump (Lufthebepumpe). Verfügbar unter: http://ca.youtube.com/watch?v=oxJTC77PADQ [Zugriff am 15. April 2010].
- ↑ Cornish Pulser Pump. Verfügbar unter: http://www.youtube.com/watch?v=Tf1-7fL_UIk [Zugriff am 15. April 2010].
- ↑ Susan J. White. „Bubble Pump Design and Performance“ Georgia Institute of Technology: August 2001. Online verfügbar unter: http://www.me.gatech.edu/energy/SusanThesis.pdf [Zugriff am 13. April 2010].
















_{Pumpe}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/186fa09ca298967fbea8a409ab958aa6a1024310)
_{Pumpe}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d95dbd316e21fe0d91aced359f606e1cbd0bca2e)

![{\displaystyle h_{Pumpe}={\frac {\rho _{Wasser}A(h_{Einlass}-h_{Auslass})}{[\rho _{Wasser}\%_{Wasser}+\rho _{Luft}\%_{Luft}]A_{Pumpe}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5130c96622af52a244433b6f4885a78aa475a126)







