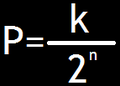.jpg)
Abstract[edit | edit source]
This page and project was created by team GID, who's members include Chris Arcani, Neil Cudney, Marjani Ellison, and Eli Wallach. GID is from HSU's spring engineering 215 class. Our selected client for the design project during the course was Zane Middle School. Our project needed to visually demonstrate probability while being safe, interactive, and aesthetically appealing. The machine that best matched our criteria is a quincunx, which fits well with STEAM. STEAM is a learning motto set for Zane Middle School which stands for: Science, Technology, Engineering, Arts, and Mathematics. The quincunx machine sorts balls by replicating pascals triangle to make out a bell curve, demonstrating probability to Zane Middle School students in multiple ways.
Background[edit | edit source]
In the fall of 2013, Zane Middle School adopted the academic program STEAM with the goal of providing students from 6th to 8th grade the skills needed for the 21st century workplace. Zane Middle School recently formed a partnership with Cal Poly Humboldt (HSU) around STEAM principles. Therefore, HSU students in ENGR-215 use their knowledge of design and engineering to build structures or visual educational demonstrations to provide middle school children hands-on experience with the subjects covered by STEAM. Team GID (Get it Done) was tasked with the building of a probability machine to provide middle school students a hands-on demonstration of the mathematical concepts of probability.
Team GID:
Problem statement and criteria[edit | edit source]
Zane Middle School focuses on the STEAM curriculum for students from sixth through eighth grade. Zane strives to give students an effective education by focusing on hands on activities. Zane Middle School asked Humboldt State's engineering 215 class to help improve their campus and teaching implements for the second consecutive term. Our goal is to design and build an effective demonstration model that helps to teach students probability in a hands on way. We made a criteria table to better reflect what our client wanted to see in our project. Our criteria is listed in the table below with a weight for the importance and a comment for the constraints.
| Criteria | Importance | Constraints |
|---|---|---|
| Educational Value | 10 | Demonstrates probability to 6-8th graders. |
| Safety | 10 | Students must not be injured by the machine. |
| Ease of Interaction | 8 | Students must take some part in using the machine. |
| Durability | 8 | Remains operational and scratch resistant. |
| Aesthetics | 6 | Attracts and keeps the attention of 6-8th graders. |
| Portability | 4 | Easily moved by one adult. |
| Ease of Implementation | 6 | Less than 10 minute set up time. |
| Cost | 6 | Does not exceed $400. |
Description of final project[edit | edit source]
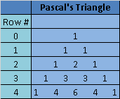
The quincunx machine teaches applications of mathematical probability. The probability of a single ball bouncing to the left on the first peg is 50%. The probability of a ball bouncing to the left many times in a row is significantly less, because there are more paths leading to the middle of the machine than there are paths leading to the sides. As a result, the balls should form a bell-shaped curve at the bottom of the quincunx. The conversion formula, shown below, is used to convert Pascal's Triangle to The Probability Triangle. In the formula, k is a number in Pascal's Triangle, and n represents the row number that contains k. By this definition of probability, probability is a number between zero and one. Each row in the probability triangle should sum to one. The larger probabilities at the center of The Probability Triangle mathematically illustrate the bell-shaped curve that forms at the bottom of the quincunx.
The machine is designed to capture the attention of middle-school students and to be seen by a large audience. The machine is three feet wide and five feet tall in order for it to be seen by large audiences. The backboard of the quincunx is made of aluminum sheeting along with the collection chute which collects the balls once the demonstration is done. The front viewing sheet is made of acrylic, and the collection chute is an aluminum box. The rubber bouncy balls used to make the curve will be one inch in diameter. The pins that the balls will bounce off of will be aluminum rods cut into two inch sections that are half an inch in diameter.
-
Pascal's Triangle
-
The conversion formula.
-
Probability Triangle
How to use[edit | edit source]
-
Step 1: Insert the balls into the top of the quincunx.
-
Step 2: The balls hit the pegs and bounce either left or right.
-
Step 3: The balls will form a bell-shaped curve at the bottom.
-
Step 4: Pull the handle on the front of the quincunx to retrieve the balls.
Costs[edit | edit source]
| Quantity | Material | Source | Cost ($) | Total ($) |
|---|---|---|---|---|
| 1 | Aluminum Sheet 15'X 5'X 1/8" | Alves Inc | Donated | 0.00 |
| 1 | Acrylic Sheet 4'X 3'X 1/4" | POP Displays | 81.00 | 81.00 |
| 150 | Marbles | Zane Middle School | Donated | 0.00 |
| 2 | Aluminum Round 1/2"X 12' | Bay Tank | 15.00 | 30.00 |
| 1 | Paint | Ace hardware | 30.00 | 30.00 |
| Total Cost | $246.60 | |||
Testing Results[edit | edit source]
The quincunx machine creates a bell curve using bouncy balls that the students place in the hopper. The machine demonstrates probability using a basic template by only using the 50/50 probability of a ball going one way or another. The continuous equal chance of the ball falling one way or the other keeps the probability easy to predict and easy to calculate. Some of the bouncy balls that have more elasticity leave the pattern and end in the outer columns.
How to build[edit | edit source]
Cut aluminum plate to size.
Cut aluminum round to pin lengths and stand off lengths.
layout grid for pins and drill holes.
weld stiffener to the back and chute details to the front.
Thread standoffs.
weld pins into backboard.
Glue, drill and install acrylic cover
Discussion and next steps[edit | edit source]
Although the quincunx machine is not the most interactive probability machine, it demonstrates the highest safety and educational value. The bouncy balls sometimes skip a few pegs, but the curve at the bottom of the quincunx still accurately represents the probability curve. The quincunx is made of durable aluminum metal, so the maintenance cost is cheap. The machine only needs to be unscrewed with a Phillips wrench and wiped with a damp rag once a month. The machine will be stored at Zane Middle School in Eureka California.
The quincunx was present at the 2015 math festival located in Eureka's Bayshore Mall on April 25th. The machine does a great job of catching the attention of both children and adults. The machine is durable enough to withstand any shaking caused by children, and children are compelled to keep guessing which chamber the next ball will land in. The only criteria is not fulfilled is the portability. The quincunx is heavier than expected, and requires two adults to move.
The bouncy balls used in the quincunx machine are going to be replaced with marbles. On many occasions, the bouncy balls bounce to the side on the first few pegs. Also, the bouncy balls stick to the inside of the machine, and can be difficult to remove.
Contact details[edit | edit source]
Any questions or comments about the machine contact GID at: csa146@humboldt.edu, esw108@humboldt.edu, mde120@humboldt.edu, nac373@humboldt.edu.
References[edit | edit source]
(Unknown) "Roulette" 12 games of chance <http://www.math.uah.edu/stat/games/Roulette.html> (February 21, 2015)
Cardinal Glass Industries. (2011). Architectural Glass Guide, Troy, Michigan.
Dan Reed "How the Game Works" Dan's Pachinko Data Page <http://faculty.ccp.edu/faculty/dreed/Campingart/pachinko/> (February 22, 2015)
Davenport, S. (2007). Designing With Laminated Glass, St. Louis, Missouri.
Isaac, Richard. Ewing, J.H., Gehring, F.W., Halmos, P.R. (1995). The Pleasures of Probability. Springer-Verlag. New York. Cars, Goats, and Sample Spaces. 2.
Joseph Hilsenrath, and Bruce F. Field(1983) "The Mathematics Teacher", Vol. 76, No. 8, 571-573
Karim Nice "How Lotteries Work" How stuff works<http://entertainment.howstuffworks.com/lottery3.htm> (February 22, 2015)
Kaysons. (Unknown). Physical Properties of Acrylic Sheets, (Unknown)
Killian, Rodney C., and Kepner, Henry S. (1976). "Pascal's Triangle and the Binomial Probability Distribution." Pasc Trig Bino Prob. 69(7). 561-563.
McGervey, John D. (1986). Probabilities in Everyday Life. Nelson-Hall. Chicago. Principles and Propositions. 1-6.
McGervey, John D. (1986). Probabilities in Everyday Life. Nelson-Hall. Chicago. Statistics. 16.
N. Chernov, and D. Dolgopyat "Journal of the American Mathematical Society", Vol22, No.3, 821-858
S.N. Ethier,(1982) "Journal of the American Statistical Association", Vol. 77, No. 379, 660-665
(UK). (Uk). "What is acrylic." Google, <http://www.google.com> (Feb. 22, 2015).
(UK). (Uk). "What is glass"." Google, <http://www.google.com> (Feb. 22, 2015).
(Unknown).(2008). "Glass vs. Acrylic Comparison." Evonik Industries, <http://www.acrylite.net> (Feb. 22, 2015)
(Unknown).(2013). "English Language Arts Standards>> Science & Technical Subjects>> Grade 6-8" Common Core State Standards Initiative, <http://www.corestandards.org/ELA-Literacy/RST/6-8/> (February 24, 2015)
(Unknown).(2014). "Library" Teaching Methods, <http://serc.carleton.edu/20966> (February 24, 2015)
(Eureka City Schools).(2015) "Zane Home" Eureka City Schools, <http://www.eurekacityschools.org> (February 24, 2015)
(Unknown).(Unknown). "Methods for Teaching Middle Schoolers - Bible Charts" Google, <http://google.com>